Presentation

Fullscreen mode

Just press »F« on your keyboard to show your presentation in fullscreen mode. Press the »ESC« key to exit fullscreen mode.

Overview mode

Press "Esc" or "o" keys to toggle the overview mode on and off. While you're in this mode, you can still navigate between slides, as if you were at 1,000 feet above your presentation.

Computational Geometry and Computer Graphics

Lesson 5

Author: Egoshkin Danila Igorevich

Plan

Vectors again
Matrices
Transformation matrices & Affine Transformation
Linear vs Nonlinear Transformations
Projection matrix
Tensors
Euler angles
Quaternions

Vectors again

Vectors

\[ \vec{v} = \begin{pmatrix} \color{#FF8080}{x} \\ \color{#80FF80}{y} \\ \color{#80C0FF}{z} \end{pmatrix} \]

Scalar vector operations

\[ \begin{pmatrix} \color{#FF8080}{1} \\ \color{#80FF80}{2} \\ \color{#80C0FF}{3} \end{pmatrix} + x \rightarrow \begin{pmatrix} \color{#FF8080}{1} \\ \color{#80FF80}{2} \\ \color{#80C0FF}{3} \end{pmatrix} + \begin{pmatrix} x \\ x \\ x \end{pmatrix} = \begin{pmatrix} \color{#FF8080}{1 + x} \\ \color{#80FF80}{2 + x} \\ \color{#80C0FF}{3 + x} \end{pmatrix} \]
Where $$+ can be +, -, \cdot or \div$$

Vector negation

\[ -\bar{v} = -\begin{pmatrix} \color{#FF8080}{v_x} \\ \color{#80C0FF}{v_y} \\ \color{#80FF80}{v_z} \end{pmatrix} = \begin{pmatrix} \color{#FF8080}{-v_x} \\ \color{#80C0FF}{-v_y} \\ \color{#80FF80}{-v_z} \end{pmatrix} \]

https://learnopengl.com/Getting-started/Transformations

Transformation: translations

\[ \vec{point} = \begin{pmatrix} \color{#FF8080}{1} \\ \color{#80FF80}{1} \end{pmatrix} \] \[ \vec{point_{new}} = \begin{pmatrix} \color{#FF8080}{2} \\ \color{#80FF80}{2} \end{pmatrix} \]

Transformation: translations

\[ \vec{point_{new}} = \begin{pmatrix} \color{#FF8080}{point_{x}} + \color{#FF8080}{T_x} \\ \color{#80FF80}{point_{y}} + \color{#80FF80}{T_y} \end{pmatrix} \]

Transformation: translations

\[ \begin{bmatrix} \color{#FF8080}{1} & \color{#FF8080}{0} & \color{#FF8080}{T_x} \\ \color{#80FF80}{0} & \color{#80FF80}{1} & \color{#80FF80}{T_y} \\ \color{#D0A0FF}{0} & \color{#D0A0FF}{0} & \color{#D0A0FF}{1} \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{#FF8080}{T_x} \\ y + \color{#80FF80}{T_y} \\ 1 \end{pmatrix} \]

Transformation: Rotation

A rotation matrix is used to rotate objects in a coordinate system. Let's rotate a point Q(1, 1) by 90 degrees counterclockwise. Given point Q = (1, 1) and rotation angle θ = 90 degrees, the rotation matrix is: \[ \vec{point} = \begin{pmatrix} \color{#FF8080}{1} \\ \color{#80FF80}{1} \end{pmatrix} \] \[ \vec{point_{new}} = \begin{pmatrix} \color{#FF8080}{-1} \\ \color{#80FF80}{1} \end{pmatrix} \]

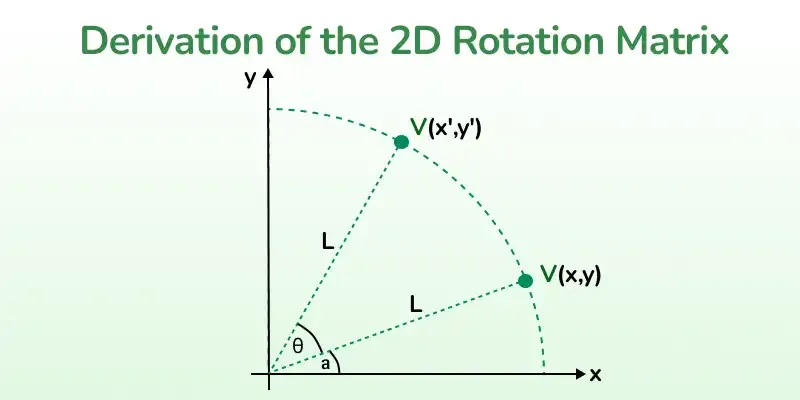
Transformation: Rotation

Expressing (x, y) in the polar form, we get: \[ \color{#FF8080}{x = L \cos a} \\ \color{#80FF80}{y = L \sin a} \]

Transformation: Rotation

Similarly, expressing (x', y') in polar form \[ \color{#FF8080}{x' = L \cos (a + θ)} \\ \color{#80FF80}{y' = L \sin (a + θ)} \]

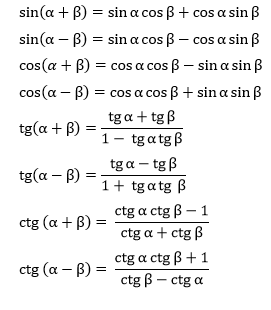
Transformation: Rotation

Using trigonometric identities we get, \[ \begin{aligned} \text{x'} = L (\cos a \cos \theta - \sin a \sin \theta) \\ = L \cos a \cos \theta - L \sin a \sin \theta \\ \end{aligned} \] Substituting the values from equations (1) and (2): \[ \text{x'} = x \cos \theta - y \sin \theta \qquad \text{(3)} \]

Transformation: Rotation

For the y-coordinate, \[ \begin{aligned} \text{y'} = L (\sin a \cos \theta + \cos a \sin \theta) \\ = L \sin a \cos \theta + L \cos a \sin \theta \\ = y \cos \theta + x \sin \theta \qquad \text{(4)} \end{aligned} \]

Transformation: Rotation

\[ \begin{bmatrix} \color{#FF8080}{\cos\theta} & \color{#FF8080}{-\sin\theta} & \color{#FF8080}{0} \\ \color{#80FF80}{\sin\theta} & \color{#80FF80}{\cos\theta} & \color{#80FF80}{0} \\ \color{#D0A0FF}{0} & \color{#D0A0FF}{0} & \color{#D0A0FF}{1} \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x \cos\theta - y \sin\theta \\ x \sin\theta + y \cos\theta \\ 1 \end{pmatrix} \]

Transformation: Affine Transformations

Affine transformations are the simplest form of transformation. These transformations are also linear in the sense that they satisfy the following properties:

Lines map to lines
Points map to points
Parallel lines stay parallel

Some familiar examples of affine transforms are translations, dilations, rotations, shearing, and reflections. Furthermore, any composition of these transformations (like a rotation after a dilation) is another affine transform.

Links:

Thanks for your attention :)